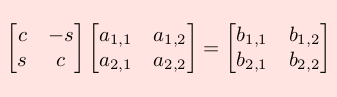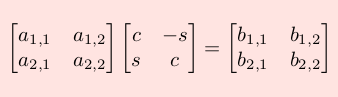Trasformazione di Givens

E' noto dalla grafica che ruotando un punto P (in questo caso considerato come estremita' del vettore OP) attorno alla origine degli assi di un certo angolo antiorario θ, si ottiene un punto Q le cui coordinate si possono esprimere nella seguente forma matriciale:

avendo posto s=sin θ e c=cos θ
In questo caso la relazione precedente non va usata per determinare le coordinate finali del punto P ruotato di un assegnato angolo θ, bensi' si desidera determinare l'angolo θ (ovvero i valori s e c) tali che il vettore ruotato {OQ} abbia una componente nulla ovvero venga fatto coincidere con uno degli assi di riferimento.
Imponendo che risulti y_Q=s·x_P+c·y_P=0 si ricava che l'angolo di rotazione da imporre risulta θ=-arctg(y_P/x_P) e quindi:

Per una matrice 2*2, a seconda che la matrice di rotazione venga usata per premoltiplicare o postmoltiplicare, si verifica una di queste 2 situazioni:

volendo annullare, in entrambi i casi, il termine b_2,1 si deve assumere nel primo caso θ=-arctg(a_2,1/a_1,1) e nel secondo caso θ=-arctg(a_2,1/a_2,2)
Per una matrice n*n c'e' piu' liberta' nello scegliere il termine ausiliario. Qui si converra' di assumere:

nel primo caso: ii=i-1 se i>1 oppure ii=n se i=0
nel secondo caso: jj=j+1 se j<n oppure jj=0 se j=n

La matrice di rotazione [G] verra' definita partendo da una matrice identica n*n e inserendovi:

nel primo caso: g_i,i=g_ii,ii=c g_i,ii=s g_ii,i=-s
nel secondo caso: g_j,j=g_jj,jj=c g_jj,j=s g_j,jj=-s

Per un esempio definire innanzitutto la matrice [A] cui applicare la trasformazione. Specificare quindi l'indice di riga i e l'indice di colonna j del coefficiente matriciale a_i,j che si vuole annullare e se si vuole una matrice che opera in premoltiplicazione o postmoltiplicazione.
Viene calcolata la matrice [G] di Givens che realizza la trasformazione nonche', per verifica, la matrice prodotto [B]=[G]*[A] o [B]=[A]*[G]

L'utilizzo del presente foglio di calcolo e' freeware, a patto di accettare le condizioni qui appresso riportate.
Per quanto si sia fatto il possibile non si puo' garantire che i valori forniti siano esenti da errori e quindi si demanda agli utenti il compito di trovare conferma per altra via sia dei risultati ottenuti che dei valori di input eventualmente proposti rigettando qualunque tipo di responsabilita' per qualsiasi tipo di danno correlabile con il suo uso. Chi non accetta la sopracitata clausola di esclusione di responsabilita' non deve usare il foglio di calcolo.