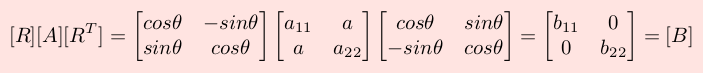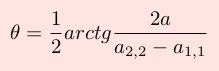Trasformazione di Jacobi

La trasformazione di Jacobi e' valida per matrici simmetriche.
Il suo scopo e' di annullare 2 termini simmetrici non appartenenti alla diagonale principale. Per una matrice simmetrica [A] 2*2 la si puo' esprimere tramite la seguente relazione:

l'angolo θ che realizza la suddetta trasformazione lo si puo' ottenere risolvendo rispetto a θ l'equazione che si ottiene uguagliando a zero il termine b_1,2 o b_2,1 della matrice [B] e risulta:

In pratica la matrice di rotazione [R], e la sua trasposta [R^T] hanno lo stesso ordine della matrice [A] da trasformare.
Volendo annullare il termine a_i,j (e il suo simmetrico a_j,i) si calcola preventivamente il valore dell'angolo θ dopodiche' si costruisce la matrice di rotazione [R] partendo da una matrice identica [I] e introducendovi i termini diagonali r_i,i=r_j,j=cos θ nonche' i termini ulteriori r_i,j=-sin θ e r_j,i=sin θ

Per un esempio immettere una matrice [A] simmetrica, definire gli indici di riga-colonna dei 2 termini da annullare e attivare il calcolo agendo sul pulsante Eval.
Viene fornita in output la matrice di rotazione [R] e , per controllo, il prodotto [B]=[R]*[A]*[R^T].
Il programma definisce la matrice da decomporre generando una matrice random e poi moltiplicandola per la trasposta.

L'utilizzo del presente foglio di calcolo e' freeware, a patto di accettare le condizioni qui appresso riportate.
Per quanto si sia fatto il possibile non si puo' garantire che i valori forniti siano esenti da errori e quindi si demanda agli utenti il compito di trovare conferma per altra via sia dei risultati ottenuti che dei valori di input eventualmente proposti rigettando qualunque tipo di responsabilita' per qualsiasi tipo di danno correlabile con il suo uso. Chi non accetta la sopracitata clausola di esclusione di responsabilita' non deve usare il foglio di calcolo.