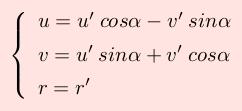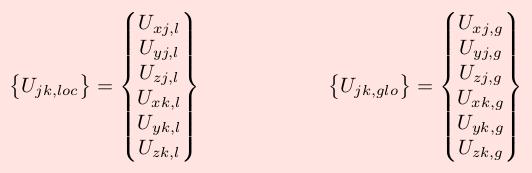Metodo della Matrice di Rigidezza - Direct Stiffness Method

Nel risolvere una struttura con il metodo della matrice di rigidezza si assume un sistema di riferimento globale O(x,y,z) destrorso e, per le varie aste, una serie di riferimenti locali destrorsi j(x',y',z') aventi l'asse x' coincidente con l'asse dell'asta e l'origine in uno dei due nodi di estremita'. In conseguenza di questa scelta l'asta dovra' essere considerata come orientata dal nodo origine i verso l'altro nodo k.

A seguito della deformazione i punti i e k vanno in due punti i' e k'. Si adotta la convenzione di segno di considerare sia gli spostamenti che le forze nodali positivi se concordi con i versi positivi degli assi di riferimento ovvero antiorari.
Consideriamo, per il momento, il solo primo nodo i e indichiamone con u, v, r le componenti di spostamento nel sistema di riferimento globale. Le corrispondenti componenti di spostamento u', v', r' nel sistema di riferimento locale si possono esprimere tramite le seguenti relazioni:

ovvero nella seguente forma equivalente:

Ma le relazioni precedenti si possono anche invertire ricavando u, v, r in funzione di u', v', r' :

Combinando in un unico vettore le deformazioni dei due nodi di estremita' dell'asta si ottengono le seguenti due relazioni per la conversione delle componenti di deformazione nodali dal sistema di riferimento globale a locale e viceversa:

avendo posto:

Adottando inoltre le posizioni:

Si puo' scrivere, piu' sinteticamente:

{U_jk,glo}=[RLTOG_jk]·{U_jk,loc}

{U_jk,loc}=[RGTOL_jk]·{U_jk,glo}

ed e' da notare che le due matrici di rotazione sono l'una l'inversa dell'altra, come risulta implicitamente dalle due ultime relazioni e come viene confermato dal calcolo diretto del prodotto matriciale:

[RGTOL_jk]·[RLTOG_jk]=[I]

essendo sin²α+cos²α=1

Anche le forze nodali di estremita' di un'asta vengono espresse tramite un vettore di due strutture ciascuna composta di 3 termini che esprimono rispettivamente le componenti in direzione x' y' o rotazionale ovvero x y e rotazionale a seconda del sistema di riferimento adottato.

inoltre si adotta la stessa convenzione di segno usata per gli spostamenti, cioe' forze nodali positive se concordi con i versi positivi degli assi di riferimento ovvero positive se antiorarie nel caso di coppie.
Dal momento che le coppie nodali di estremita' sono indipendenti dal sistema di riferimento, come lo erano le rotazioni, valgono relazioni di legame tra componenti locali e globali del tutto analoghe alle precedenti e risulta, in definitiva:

{F_jk,glo}=[RLTOG_jk]·{F_jk,loc}

{F_jk,loc}=[RGTOL_jk]·{F_jk,glo}

Le matrici di rigidezza di un elemento strutturale sono, per definizione, delle matrici tali che moltiplicate per il vettore degli spostamenti dei due nodi di estremita' forniscono il vettore delle forze nodali di estremita' in grado di determinare quel certo vettore di spostamenti. Esse dipendono dal sistema di riferimento. Si puo' scrivere:

{F_jk,loc}=[KLOC_jk]·{U_jk,loc}

{F_jk,glo}=[KGLO_jk]·{U_jk,glo}

Dalla precedente definizione, relativa al sistema di riferimento locale, si vede che assumendo un vettore di deformazione avente tutte le componenti nulle eccetto una assunta unitaria, il corrispondente vettore delle forze coincide con i coefficienti della matrice di rigidezza posti sulla colonna avente lo stesso indice del termine unitario del vettore {Uik,loc} (unico termine non nullo).
Pertanto per determinare la matrice di rigidezza di un'asta nel sistema di riferimento locale occorre compiere le seguenti operazioni:

• svincolare uno dei nodi terminali secondo una certa componente di spostamento applicando una corrispondente forza positiva
• risolvere il sistema iperstatico determinando il valore che deve avere la forza introdotta per determinare uno spostamento unitario (questo sara' il termine diagonale)
• determinare le corrispondenti reazioni vincolari, definendone il segno in base al sistema di riferimento adottato

In sostanza si tratta di risolvere 6 sistemi iperstatici determinando complessivamente 36 coefficienti. Questo calcolo viene solitamente fatto trascurando il contributo della deformazione a taglio. Si arriva cosi' a definire, nel sistema di riferimento locale, una matrice simmetrica di questo tipo:

Avendo posto:

Sostituendo nella relazione {Fjk,loc}=[KLOCjk]*{Ujk,loc} le espressioni dei vettori locali in funzione dei vettori globali, si ottiene:

[RGTOL_jk]·{F_jk,glo}=[KLOC_jk]·[RGTOL_jk]·{U_jk,glo}

premoltiplicando per [RGTOL_jk]^-1=[RLTOG_jk] :

{F_jk,glo}=[RLTOG_jk]·[KLOC_jk]·[RGTOL_jk]·{U_jk,glo}

ossia:

[KGLO_jk]=[RLTOG_jk]·[KLOC_jk]·[RGTOL_jk]

Quest'ultima relazione consente di esprimere la matrice di rigidezza globale di un'asta in funzione della matrice di rigidezza locale e delle matrici di rotazione. Le operazioni di calcolo sono abbastanza contenute da consentire anche un calcolo parametrico diretto. Si ottiene:

avendo qui posto, per brevita', s=sin(alfa) e c=cos(alfa).
Definite le matrici di rigidezza globali [KGLOik] delle varie aste costituenti la struttura si deve arrivare a definire la matrice di rigidezza della intera struttura [KSTRU] assemblando le varie matrici [KGLOik].
Per quanto detto in precedenza siamo in grado di esprimere la matrice di rigidezza di una generica asta della struttura nel sistema di riferimento globale e possiamo scrivere:

{F_jk,glo}=[KGLO_jk]·{U_jk,glo}

Per costruire la corrispondente equazione relativa alla intera struttura dobbiamo pensare di scrivere la precedente equazione per tutte le aste eseguendone l'assemblaggio in base a questi criteri:

• i vettori {F_jk,glo} (che sono di 6 termini e rappresentano le forze esterne nodali agenti nei nodi terminali dell'asta j-k) vanno assemblati in un vettore {F} di 3*n termini sommando i valori che aste diverse apportano come contributo in ogni nodo e secondo la medesima componente di sforzo
• i vettori {U_jk,glo} (che sono di 6 termini e rappresentano le componenti di spostamento nodali dei nodi terminali dell'asta j-k) vanno assemblati in un vettore {U} di 3*n termini senza effettuare alcun cumulo perche' si tratta di imporre la congruenza degli spostamenti nodali in tutti i nodi della struttura
• le matrici [KGLO_jk] (che sono matrici 6*6 e rappresentano le rigidezze dei nodi terminali della singola asta j-k) vanno cumulati in somma nella matrice di rigidezza [KSTRU] della intera struttura (che e' una matrice 3n*3n). E' in questo caso necessario effetture il cumulo in somma perche' ogni termine di rigidezza nodale viene ad essere incrementato al crescere del numero di aste che confluiscono nel nodo. Se si conviene di assemblare a gruppi di 3 sia le equazioni di equilibrio nodali (equilibrio alla traslazione in direzione x, equilibrio alla traslazione in direzione y, equilibrio alla rotazione attorno all'asse z) che le componenti di spostamento nodali (ξ, η, φ) i coefficienti di indicizzazione da utilizzare per la locazione in somma relativi ai vari termini della matrice di rigidezza globale [KGLO_jk] della generica asta j-k sono quelli desumibili dalla seguente tabella:

Ad assemblaggio eseguito si ottiene l'equazione:

{F}=[KSTRU]·{U}

che puo' essere riscritta nella forma:

[KSTRU]·{U}={F}

vedendola come il sistema risolvente per una struttura sottoposta solo a carichi nodali.
Nella precedente equazione {F} e' il vettore delle forze nodali esterne agenti sui vari nodi della struttura. Per una struttura soggetta anche a carichi agenti lungo le aste si devono mettere in conto anche le corrispondenti azioni nodali. Essendo queste uguali e contrarie alle reazioni di incastro perfetto l'equazione diventa:

[KSTRU]·{U}={F} - {F}

ove, a termine noto {TN}={F}-{F}, il vettore {F} e' un vettore di 3n termini che rappresenta le forze nodali esterne agenti sui nodi della struttura (definite con il segno positivo se concordi con il verso positivo nel sistema di riferimento globale Oxy) mentre il corrispondente termine soprassegnato rappresenta la risultante nodale delle reazioni di incastro perfetto per tutte le aste confluenti in un dato nodo a patto di aver valutato queste reazioni come azioni dei vari nodi sulle sezioni terminali delle corrispondenti aste.

La locazione dei termini noti a secondo membro della precedente equazione deve avvenire in base al seguente schema di indicizzazione:

essendo le varie sommatorie estese a tutte le aste confluenti nel nodo j per cui si stanno scrivendo i valori a termine noto.
Possiamo pertanto concludere che per risolvere un sistema strutturale con il metodo della matrice di rigidezza occorre compiere le seguenti operazioni:

• definire la matrice di rigidezza della struttura [KSTRU] tramite assemblaggio delle matrici di rigidezza, nel sistema di riferimento globale, delle varie aste che la compongono
• assemblare il vettore dei termini noti facendo la differenza tra il vettore delle forze nodali esplicite e quello delle forze nodali equivalenti ai carichi non nodali agenti sulle aste
• imporre le condizioni al contorno, relative ai nodi vincolati, variando certi coefficienti in oppotune rigne della matrice [KSTRU] nonche' il corrispondente coefficiente di rigo nella colonna dei termini noti {TN}
• risolvere il sistema lineare modificato determinando il vettore degli spostamenti nodali {U} della intera struttura
• calcolare le forze nodali alle estremita' delle varie aste, nel sistema di riferimento globale, tramite la relazione {F_jk,glo}={F_jk,glo}+[KGLO_jk]·{U_jk,glo} (essendo {U_jk,glo} il vettore degli spostamenti nodali delle estremita' dell'asta j-k ottenibile assemblando le due terne di valori esprimenti le deformazioni relative ai nodi j e k estratte dal vettore {U} degli spostamenti nodali relativo alla intera struttura)
• calcolare le forze nodali alle estremita' delle varie aste, nel sistema di riferimento locale, tramite la relazione {F_jk,loc}=[RGTOL_jk]·{F_jk,glo}

La matrice [KSTRU] costruita tramite assemblaggio e' relativa ad una struttura avente tutti i nodi liberi e percio' labile. Per introdurre le condizioni al contorno si potrebbe procedere eliminando, in [KSTRU] e {TN}, le righe che corrispondono alle equazioni di equilibrio relative alle componenti di spostamento nulle o note, e introducendo il valore della componente di spostamento nulla o nota nelle restanti equazioni con conseguente variazione anche dei termini noti. Procedendo in questo modo si riduce il numero delle incognite del problema ma si e' costretti a riorganizzare numericamente e dimensionalmente sia la matrice [KSTRU] che il vettore {TN} e, soprattutto, si perde la corrispondenza immediata tra componente di spostamento e indice di rigo della corrispondente equazione di equilibrio nodale.
Il programma di calcolo utilizza il metodo alternativo di non ridurre il numero delle incognite ma conservare, modificandole, le righe corrispondenti alle equazioni di equilibrio relative alle componenti di spostamento dei nodi vincolati. Si adottano questi criteri di modifica:

• se un nodo e' vincolato perfettamente secondo una certa componente di spostamento, onde imporre che lo spostamento del nodo sia nullo, viene modificata la riga corrispondente della matrice [KSTRU] annullando tutti i termini eccetto quello diagonale che va posto pari a 1, inoltre nel vettore {TN} il corrispondente termine va posto a 0
• se un nodo e' vincolato plasticamente secondo una certa componente di spostamento, onde imporre che lo spostamento del nodo sia pari al valore del cedimento plastico, nella riga corrispondente della matrice [KSTRU] si annullano tutti i termini eccetto quello diagonale che viene posto pari a 1, inoltre nel vettore {TN} il corrispondente termine va posto pari al valore noto u* del cedimento plastico
• se un nodo e' vincolato elasticamente secondo una certa componente di spostamento e' come se fosse libero ma occorre tener conto di una forza aggiuntiva elastica, sul nodo, dovuta alla reazione elastica del vincolo. Tale termine aggiuntivo, essendo una forza nodale, andrebbe collocato a secondo membro ove dovrebbe assumere il segno negativo in quanto ad uno spostamento in direzione positiva corrisponde una reazione elastica sul nodo di verso opposto e percio' negativa. Tuttavia tale forza nodale non e' nota ma ha un valore proporzionale allo spostamento del nodo, ovvero alla incognita corrispondente al termine diagonale, e pertanto deve essere collocato a primo membro in somma al valore del coefficiente del termine diagonale di rigo nella matrice di rigidezza [KSTRU]. In definitiva, nel caso di nodo vincolato elasticamente, i coefficienti nella riga corrispondente della matrice [KSTRU] vanno lasciati tutti invariati eccetto quello diagonale al quale deve essere portata in somma la costante elastica c* del vincolo, inoltre il termine corrispondente nel vettore {TN} va lasciato invariato.

Procedendo in questo modo accade che un termine deformativo con valore noto viene fatto rientrare come incognita in un procedimento di calcolo iterativo. Ne conseguono dei valori finali che non sono proprio pari al valore, nullo o noto, della deformazione nodale. Il programma elimina tale difformita' forzando questi particolari valori proprio ai valori noti.

---

Per quanto si sia fatto il possibile non si puo' garantire che il prodotto (intendendo per tale qualunque file incluso nel pacchetto di installazione e non soltanto il file eseguibile) sia esente da errori e quindi si demanda agli utenti il compito di trovare conferma per altra via sia dei risultati ottenuti con l'uso del programma che di qualunque indicazione rilevabile dai file annessi al prodotto rigettando questo e qualunque altro tipo di responsabilita' per qualsiasi tipo di danno correlabile con l'uso del prodotto. Chi non accetta la sopracitata clausola di esclusione di responsabilita' non deve usare il prodotto.